Inwit Publishing, Inc. and Inwit, LLC -- Writings, Links and Software Demonstrations

INWIT™ — HISTORY AND ODDITIES OF THE NUMBER PI

Publications in Science and Mathematics, Computing and the Humanities
Museum Development, Educational Curricula, and Science Fair Initiatives
Educational Toys and Technology

History and Oddities of the Number Pi

by Vincent Mallette
Copyright © 1999 Inwit Publishing, Inc.
Journal of the Tennessee Academy of Science

Volume 37, Number 4, October, 1962

HISTORY AND ODDITIES OF THE NUMBER p (1)

Vincent Mallette

[This paper was among the first in the flood of p -mania research.

It has been massively updated by the author since its

original publication 36 years ago — VM]

"We have compared the probability that an unknown savant has solved the problem with the probability that there is one madman the more on the earth. The latter appears to us the greater."

— The French Academy, in explaining why it would accept no more memoirs on circle-squaring

Genius is a superior aptitude to patience.

— Georges Buffon

p = 3.14159265358979...

Ö 10 = 3.162277660168...

3¹/₇= 3.142857142857...

— For reference while reading this paper

[The hard-copy version of this paper contains 7,800 places of p — 390 digits printed in 4-point type on the right-hand margin of every page. From a distance the thin string of tiny numbers looks like an ornamental border, but up close every digit is readable. Altogether the 7,800 places of p stretches for over 16 feet. It is sobering to realize that this precision of p was not available until 1958 — indeed 390 places were not available until 1853.]

Daisuke Takahashi and Yasumasa Kanada of the University of Tokyo have computed p to over 51 billion places of decimals (2). By contrast, the ancient Babylonians and Hebrews flourished and died believing that p was a simple 3 (3). The Egyptians, we deduce from one of their papyri, knew 3.16(4), but implicit in their Great Pyramid is the even better value 3.14 (5). The early Hindus and Chinese were content with 3 (6). The Greeks, in the person of Archimedes, fixed p ’s limits as >3.141 and <3.143. The Romans rolled over all the world in chariots whose wheels they believed to be exactly 3.125 times as far around as they were across (7). The later Greeks, in the person of Ptolemy, knew 3.1416 (8). In the 5th century A.D. Tsu Ch’ung-chih, a Chinese mechanician who is credited with constructing a motor boat (9), gave p correct to six decimals (10) — an accuracy which was not equaled in the western world for 1000 years (11). St. Thomas Aquinas, if he had had occasion to measure terrestrial circles, would have used the square root of 10 for p — and he would have been told that the square root of 10 was equal to 3¹/₇! (12) The Hindus during the A.D. period were also fond of the square root of 10 (13); their best value, however, was 3.1416, given by Aryabhata, but this number may have been inherited from Ptolemy (14).

The Hebrew value of 3 is deduced from two passages in the Old Testament (15) which give the diameter and circumference of a 15-ft. circular vessel in Solomon’s temple. This value is repeated, by the way, in the Jewish Talmud (16). The Great Pyramid, in case you’ve been wondering, provides its putative value of p in the form of the ratio between one-half its perimeter and its height; this ratio is about 3.14, depending on whose measurements you use. (Unlike so many other "Great Truths from the Great Pyramid," this one is not thought to be the result of mere numerological jiggery-pokery.)(17) Archimedes (around 225 B.C.)(18) obtained his celebrated limits for p by considering the perimeters of inscribed and circumscribed polygons having 96 sides. Calculating these perimeters involved enormous labor, for Archimedes did not have Arabic numerals and therefore met with great difficulty in extracting square roots, which were essential in his process (19). The method employed by Tsu Ch’ung-chih for his six correct digits is not known for sure, but may have been similar to Archimedes’ (20). In 1579 Francois Vieta, the man who introduced literal quantities into algebra, used polygons of 393,216 sides to obtain p to 9 correct places (21). The polygon method reached its apex in 1610, when the German monomaniac Ludolph van Ceulen calculated p to 35 places by means of a polygon with 4 quintillion, 611 quadrillion, 686 trillion, 18 billion, 427 million, 387 thousand, 904 sides (22). Van Ceulen worked on this computation up until the time of his death (23), whereupon the 35 places, which was as far as he had gotten, were inscribed on his tombstone (24). Today in Germany p is still sometimes known as the Ludolphian number (25), in honor of this deluded man (26). In 1621 Willebrord Snell, the traditional discoverer of the law of refraction, duplicated Van Ceulen’s vaunted result with a polygon of a mere billion sides (27). Snell’s method was so superior that he obtained a value as good as Archimedes’ from a common hexagon (28). Christian Huygens gave a correct proof of the validity of Snell’s short cut (29).

Vieta in 1593 gave the first non-geometrical method for finding p (30), in the form of the infinite continued product

(2/p) = (Ö ˝)´ (Ö (˝ + ˝Ö ˝))´ (Ö (˝ + ˝Ö (˝ + ˝ Ö ˝)))´ × × × ×

By the middle of the 17th century, infinite processes like Vieta’s began to dominate the p -computing field. John Wallis, in 1656, proved(31) that

(p/2) =
_{2 ·
2 ·
4 ·
4 ·
6 ·
6 ·
8...

1 ·
3 ·
3 ·
5 ·
5 ·
7 ·
7...}

Viscount Brouncker, a few years earlier, had proposed (32) the series

(4/p) = 1 + 1˛/2 + 3˛/2 + 5˛/2 + _{· · · ·}

I should mention that "by 1666 Newton had found a way to calculate p , using his binomial theorem, to 16 decimal places using only 22 terms of an infinite series expansion."(33)

Simplest of all series (34) was that given by Leibniz (35) in 1682,

(p/4) = 1 – ¹/₃ + ¹/₅– ¹/₇ + _{· · · ·}

Leibniz’ series is, however, a special case of the series discovered by James Gregory (36) in 1670, probably the most important series in the history of p :

arctan x = x – (x³/3) + (x⁵/5) – (x⁷/7) + _{· · · ·}

Around 1700 John Machin, an English mathematician and professor of astronomy at Gresham College, London, established (37) his important formula

(p/4) = 4 arctan ¹/₅ – arctan ¹/₂₃₉

Machin’s formula, together with Gregory’s series, provided the mathematical tools for virtually every p calculator from 1700 until the beginning of the computer era. In the next 150 years at least nine men, independently, each carried the value of p to over 100 places. In 1840 the sixteen-year-old German prodigy Zacharias Dase calculated p to 200 places, in only two months (38). Dase was perhaps the most phenomenal mental calculator who ever lived (39); working in his head, he once obtained the product of two 8-digit numbers in less than a minute, and did the same for two 40-digit numbers in 40 minutes (40). His last years were spent in factoring the numbers between 7,000,000 and 10,000,000, a job which he had half completed when he died at the age of 37 (41).

Most famous of all p calculators was of course William Shanks, who boldly went where no man had gone before — 707 places. Starting in 1850 (42), when he was 38 years old, Shanks had by 1853 obtained 607 places, and published the result at his own expense (43). By 1873 he had extended the computation to the historic 707th place, and in the following year made a revision of his calculation. Shanks did not work continuously on the monster project; in his own words (44), "[The Author] was anxious to fill up his scanty intervals of leisure with the achievement of something original, and which, at the same time, should not subject him to either too great tension of thought or to consult books." Writing in the third person again, Shanks observed that "the accomplishment of his purpose would add little or nothing to his fame as a Mathematician, though it might as a Computer...." (45) It did indeed add to his fame as a computer; for many years he was recognized as having made the most fabulous calculation in all history (46). Ripley included the result in one of his Believe It or Not books (47). However, in thus singling out Shanks as the all-time champion calculator, I think posterity has done scant justice to Wolfram, the Dutch lieutenant of artillery who, a century prior to Shanks, calculated the logarithms of 10,000 numbers to 48 decimal places (48). Not to mention "Mad Mansell," who computed logarithms to 110 places in the 1930’s — millions of hand-crafted transcendental digits in the pre-computer age.

As all you computer nerds out there know, even desktop PC’s today can churn out hundreds of places of p (49) in a few minutes with suitable algorithms. A garden-variety supercomputer, after being programmed with the problem, could do all of Shanks’ work in one-thousandth of a second (50), which is about 500 billion times faster than Shanks did it (51). Even Dase, I think, would be impressed by this speed!

There is something I have not told you. In spite of his revision of 1874, Shanks overlooked an error in the 528th place of his result. This was discovered in 1946 by Dr. D. F. Ferguson, who for some reason was doubtful of Shanks’ value and was making a calculation of his own. Ferguson used the modern formula

(p/4) = 3 arctan Ľ + arctan ¹/₂₀ + arctan ¹/₁₉₈₅

Shanks, incidentally, used Machin’s old formula.

* * *

The popular belief that the digits of p will "repeat" or "come out even" if the calculation is carried far enough, is based on a misunderstanding of number. My eighth-grade arithmetic teacher thought that p was exactly 3¹/₇, and the digits shown in the "advanced" books were simply the expansion of ¹/₇. However, it can be proved pretty simply that any decimal fraction made by dividing one whole number into another will eventually terminate or repeat. For example, as displayed in the headnote to this article, ¹/₇ when rendered into a decimal repeats with a period of 6 places. And the same is true of any fraction made of finite integers. These fractions are rational numbers, just as are the integers themselves. It’s a different story, though, for numbers like the square root of 2. These numbers may be the exact solutions of equations, but they can never be expressed exactly with any combination of integers. Even the ancients learned this to their dismay. Hippacos of Metapontum, a member of the Pythagorean Brotherhood, discovered around 450 B.C. that the side of a square will never "fit" into the diagonal: the diagonal is irrational. However, it took until 1768 for Johann Lambert (52) to prove that p was of this ilk — it could never be expressed as the quotient of two integers; it would never end as a decimal (53). Still open was the possibility that p could be an exact solution of an algebraic equation with integer coefficients. This was the door that let in the "circle-squarers," for a line constructed with straightedge and compass "implies that its length is the solution to such an equation."(54) For 114 years every kind of crank marched through this door, bearing his proof of the squared circle. Finally, in 1882, using tricky reasoning that is beyond the scope of this paper (55), Ferdinand Lindemann showed that p is not only irrational, it is transcendental (56) — it can never be the root of an algebraic equation. The French Academy was vindicated.

* * *

If the digits in the expansion of p occur at random, then, in a sufficiently long stretch of p , each digit 0-9 should appear about the same number of times. However, in Shanks’ long-standing 707-place value the number 7 is strangely slighted; it appears far fewer times than any other number. Numerological numbskulls made much of this, but the explanation is simple — Shanks’ mistake in the 528th place give rise to a systematic error which discriminated against 7’s. The new machine-calculated values have restored the missing 7’s, and p is now said to have passed all tests for randomness (57). Indeed, many hackers use p to generate random, or at least pseudo-random, numbers.

Now, if this be true, that p is completely random, then every conceivable sequence of numbers must somewhere occur in p . That is, if one considers any number, 12345678 for instance, that number will sooner or later be found in p if the search is pressed far enough. To assume otherwise would be to prejudice the randomness of p . Now anything written can be represented in numbers by using the crude cipher A = 1, B = 2, C = 3, etc., with zeros being put in to separate words. On this basis there is a particular string of numbers that corresponds to the text of, say, War and Peace, and this string will somewhere be found in p . Another "slice of p " will contain the text of every speech given in Congress last year, and for that matter every speech to be given next year (58). All this infinite material is of course indexed somewhere in p , but unfortunately the index is also infinite (59).

Those of us who do not aspire to mastering every digit in p may perhaps be satisfied with some mnemonic, which would provide, say, 30 of its decimals, thereby enabling us to compute the circumference of the universe to a hundred-thousandth of an inch (60). Here is one such mnemonic, and in verse to boot (count the letters in each word)(61):

3 1 4 1 5 9

Now I, even I, would celebrate

2 6 5 3 5 [etc.]

In rhymes inapt the great

Immortal Syracusan, rivaled nevermore,

Who in his wondrous lore,

Passed on before,

Left men his guidance how to circles mensurate.

Here’s another old favorite for remembering p : "How I want a drink, alcoholic of course, after the heavy chapters involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard...."(62) There is a French mnemonic(63) that gives p to 30 places. George Gamow has used it all his life, but unfortunately his version contains seven errors, a circumstance which has caused him trouble in at least one Scientific American article (64). The ultimate p mnemonic seems to be the famous Cadaeic Cadenza, by Mike Keith, which provides some 3835 decimals. You can pick it up at [http://users.aol.com/s6sj7gt/cadtext.htm]. Mike also has a (non-poetic) 402-place monster at [http://www.astro.univie.ac.at/~wasi/PI/pipoem402.html] (65). There are p mnemonics from all over the world at [http://www.unipissing.ca/topology/z/a/a/a/26.htm].

Georges Buffon, a French biologist who wrote a 36-volume natural history and made a translation of Newton (66), proved in 1760 (67) that if a needle of length l be cast across ruled lines separated by the distance a, the probability that the needle will lie across one of the lines

is (68)

(2 l ) /(p a). A certain Ambrose Smith in 1855 made 3,204 trials with Buffon’s method and obtained (69)^p as 3.1553. The Italian mathematician Lazzerini in 1901 executed 3,408 tosses and claimed to have achieved p correct to 6 places (70). Lazzerini has since been regarded with suspicion (71). In more modern times Michael Lloyd of Henderson State University threw needles at the rate of 150/minute for 17,000 throws and obtained 3.1394 in March of 1998. See [http://www.hsu.edu/faculty/lloydm/ti/82/buffon.82] and [http://www.mste.uiuc.edu/reese/buffon/buffon.html].

Another relation between p and probability is this: if two numbers are written down at random, the probability (72) that they will have no common divisors is 6/p ˛. With this in mind, 362 pairs of numbers were solicited from students in physics classes, and on the basis of these data your author calculated p as 3.04, a value which would qualify him to build Solomon’s temple, but not the Pyramids.

Various Oddities

· In 1897 a bill to fix the value of p at 4 was passed by the House of the Indiana state legislature (73). The bill was referred to the state senate, where it seemed sure of passage, but in the meantime various newspapers had made the legislature such an object of ridicule that the Senators decided to shelve the bill indefinitely. This turn of events especially disappointed the State Superintendent of Public Instruction, who had been hoping to secure the use, free, of the new copyrighted value of p for his state textbooks. "The case is perfectly simple. If we pass this bill which establishes a new and correct value of p , the author offers our state without cost the use of this discovery and its free publication in our school textbooks, while everyone else must pay him a royalty." [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/omlink1/html/node1.html]

The law is worded in a very obscure way that mentions neither p nor the number 4, as follows:

Be it enacted by the General Assembly of the State of Indiana: It has been found that a circular area is to the square on a line equal to the quadrant of the circumference, as the area of an equilateral rectangle is to the square on one side....

This amounts to calling p 4, as you can prove to your satisfaction by transforming the legislature’s words into an algebraic formula, bearing in mind that an "equilateral rectangle" is merely a square. Geometrically the whole thing is equivalent to saying that a circle and a square have equal areas if they have equal perimeters (74), which, of course, is ridiculous (it is a forced-draft "squaring of the circle"). The Guinness Book of Records lists this legislative lunacy as the "most inaccurate version of pi." (75) Appropriately enough, when the House began its deliberations on the bill on Jan. 18, 1897, it was exactly the full moon.

Astoundingly there are mathematicians who think this whole episode never happened, that it’s a "mathematical urban tale." Supposedly the famous story is debunked in a book published in 1992 by the Mathematical Association of America called Mathematical Cranks, by Underwood Dudley. But I haven’t been able to get hold of this book, and meanwhile the acceptance of the story by Guinness validates it for me. Furthermore, a skeptic sent away to Indiana in 1994 for a copy of the fatal 1897 bill, and obtained it without any problem. The text is exactly as my sources indicate. There’s so much controversy about this matter that I think I’m going to have to reproduce the whole body of the bill in this footnote (76). No reason not to believe the story (77)

· Albert Einstein was born on March 14 — Pi Day!

· Hoene Wronski, the Polish mathematician who gave his name to the Wronskian determinant used in differential equations, asserted that the "absolute meaning of the number p " is given by (78)

4 ¥ i^-˝[(1 + i)^1/¥ - (1 - I)^1/¥]

This of course is a farrago of nonsense; no one knows if Wronski intended this expression to be taken seriously.

· The 8-decimal value of p given in The World Almanac 1997...is incorrect! There it is (79), in all its wrongness, on the top of page 607. It’s plain to see that nerds don’t often consult this book, or there would have been an outcry. Not so many years ago the WA got in trouble for printing the wrong phases of the moon (WA’s forte), and that gaffe was written up in national newspapers. Shame!

· The sum of the squares of the reciprocals of the natural numbers (1, 2, 3, ...) is equal (80) to p ˛/6. That is, p ˛/6 = (1/1)˛ + (1/2)˛ + (1/3)˛ + ...

This is a good formula for an amateur with a desk calculator to use, if you want to try your hand at computing p . If you’re conversant with C, you can try this: It’s a 160 character C program, written by Dik T. Winter at CWI, and it computes p to 800 decimal digits.

int a=10000,b,c=2800,d,e,f[2801],g;main(){for(;b-c;)f[b++]=a/5;

for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c;d+=f[b]*a,

f[b]=d%--g,d/=g--,--b;d*=b);} (More details at:

[http://daisy.uwaterloo.ca:80/~alopez-o/math-faq/mathtext/node12.html#SECTION005100000000000000000])

· The formula

e^pi + 1 = 0

contains every fundamental quantity and relationship in mathematics: e, p , i, plus, 1, equals, 0, and minus (if the 1 be transposed to the other side). Felix Klein is supposed to have remarked that all analysis is centered here (81).

· In 1892 "a writer announced in the New York Tribune the rediscovery of a long lost secret which leads to 3.2 as the exact value of p . The lively discussion following this announcement won many advocates for the new value."(82) — Howard Eves, An Introduction to the History of Mathematics (83).

· Square the circle? Nothing to it! Jerome Meyer gives a construction for a square that matches the area of a given circle to one part in 9,000,000. Of course, this is surveying, not mathematics. Still, the Indiana legislature should have had Dr. Meyer on their side! He also trisects the angle. [Fun with Mathematics (Cleveland: World Publishing, 1952), pp. 161-164]

· Amusingly, it was considered news in 1949, when the famous ENIAC computer ground for 70 hours and computed p to ... a pitiful 2037 places of decimals! (84)

· The great self-taught Indian mathematician Srinivasa Ramanujan developed a formula for p which adds eight digits with every term (85). This is an amazing example of efficiency. I don’t have the graphics to reproduce it, but you can pull it up at [http://www.users.globalnet.co.uk/~nickjh/Pi.htm].

· p can be calculated in terms of Fibonacci numbers! Here’s one approach:

p /4 = arctan(1/Fib1 ) + ...

= arctan(1/Fib3) + arctan(1/Fib4) + ...

= arctan(1/Fib3) + arctan(1/Fib5) + arctan(1/Fib6) + ...

= arctan(1/Fib3) + arctan(1/Fib5) + arctan(1/Fib7) + arctan(1/Fib8) + ...

= arctan(1/Fib3) + arctan(1/Fib5) + arctan(1/Fib7) + arctan(1/Fib9) + arctan(1/Fib10) + ...

Thank you, Dr. R. D. Knott! (86)

· There are now many search engines for p that enable you to find a particular string of digits — your birthday, 2000, 12345 — whatever strikes your fancy. The most complete one I know gives you access to 50 million digits: [http://www.aros.net/~angio/pi_stuff/piquery.html]

Notice the run of six 9’s at place 762; that’s called the Feynman point, and is a little unexpected. Poor Shanks, for all his labor, never got to see this curiosity.

· You may as well know that there are only three ways to compute p (aside from going out and measuring a bicycle tire with a ruler). Thanks are due to Alex Lopez-Ortiz for this summary:

"1.One of the oldest is to use the power series expansion of atan(x) = x - x^3/3 + x^5/5 - ... together with formulas like pi = 16*atan(1/5) - 4*atan(1/239). This gives about 1.4 decimals per term.

2. A second is to use formulas coming from Arithmetic-Geometric mean computations. (A beautiful compendium of such formulas is given in the book pi and the AGM...) They have the advantage of converging quadratically, i.e. you double the number of decimals per iteration. For instance, to obtain 1,000,000 decimals, around 20 iterations are sufficient. The disadvantage is that you need FFT type [Fast Fourier Transform] multiplication to get a reasonable speed, and this is not so easy to program.

3.A third one comes from the theory of complex multiplication of elliptic curves, and was discovered by S. Ramanujan. This gives a number of beautiful formulas, but the most useful was missed by Ramanujan and discovered by the Chudnovskys. It is the following (slightly modified for ease of programming):

Set k_1 = 545140134; k_2 = 13591409; k_3 = 640320; k_4 = 100100025; k_5 =

327843840; k_6 = 53360;

Then pi = (k_6 sqrt(k_3))/(S), where

S = sum_(n = 0)^oo (-1)^n ((6n)!(k_2 + nk_1))/(n!^3(3n)!(8k_4k_5)^n)

The great advantages of this formula are that

1) It converges linearly, but very fast (more than 14 decimal digits per term).

2) The way it is written, all operations to compute S can be programmed very simply.

This is why the constant 8k_4k_5 appearing in the denominator has been written this

way instead of 262537412640768000. This is how the Chudnovskys have computed

several billion decimals." [For more details see site below]

[http://daisy.uwaterloo.ca:80/~alopez-o/math-faq/mathtext/node12.html#SECTION005100000000000000000]

Bailey and the Borweins, great p calculators all, have capsulized these methods as follows:

i) Archimedes’ Method

ii) Calculus-Based Methods

iii) Transformation Methods

You can read about them to your heart’s content at [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/paper.html]

· The big news, of course, in p research, is the wondrous hexadecimal algorithm of David Bailey, Peter Borwein, and Simon Plouffe (87). With this formula they can compute the ten billionth digit in the hexadecimal expansion of p — without having to calculate all the preceding n - 1 digits. "No one had previously even conjectured that such a digit-extraction algorithm for Pi was possible." (88) So far the experts can’t figure out how to apply this trick to base-10. So if we want to know the trillionth decimal digit of p , we’ll have to calculate a trillion minus one digits first!

The Symbol p

For more than half of recorded history the number which we now call p was a shadow quantity: people did not know that circumference bears a constant ratio to diameter, and the values of p which I have cited from these earliest times have had to be inferred from accounts of actual physical measurements undertaken by the ancients and from the implications of geometrical constructions. Around 225 B.C. Archimedes recognized p as a particular mathematical entity. No longer a shadow quantity, p was still an anonymous quantity, for there was no symbol to denote it. This condition prevailed for nine-tenths of recorded history.

The first number ever associated with the Greek letter p was the somewhat irrelevant 80, which was the arbitrary value of p in the Greek system of numeration (89). In 1647 William Oughtred, the inventor of both the straight and circular slide rules (90), used p to represent the circumference of a circle (91); for the ratio of circumference to diameter he used p / d , evidently, by the choice of these symbols, meaning to suggest the words periphery (i.e. circumference) and diameter (92). Isaac Barrow, Newton’s tutor, followed Oughtred’s symbolism (93). David Gregory, the nephew of the Gregory who devised the famous series, used p /r for the ratio of circumference to radius (94). p , as a single symbol to denote the ratio of circumference to diameter, rather than just circumference, appears first in a book printed in 1706 (95). The book was the Synopsis Palmariorum Matheseos, a compilation of mathematical knowledge for the general reader written by the English mathematician William Jones. Without any fanfare p , in its historic new role, turns up on page 243 of Jones’ work, where, in parentheses, it follows the notation "˝ Periphery" (96). We know that Jones’ p is the same as our modern p because twenty pages later he explicitly states that it is equal to 3.14159.... The symbol occurs at least nine times in the Synopsis, always in the modern sense, so far as we can tell from the context.

Jones’ choice of p for the circle ratio did not effect its universal acceptance. John Bernoulli used c (97); Euler used p in 1734 (98). In 1736 Euler used c (99), but the next year he adopted p (100). Christian Goldbach, the man who conjectured that every even number is the sum of two primes, used p in 1742 (101). In his monumental Analysis of 1748 Euler put vacillation aside and settled on p once and for all. After that the usage became customary (102), so customary, in fact, that people no longer remember p ’s original meaning of periphery.
Afterword:

Is there any point in calculating p to vast numbers of decimals — billions, trillions? You bet! Aside from the purely mathematical interest (will the distribution remain random, for instance), there is the fact that executing p algorithms provides a severe, one mathematician said unforgiving, test of computer software and hardware. Cray, for one, regularly tests their new models by calculating p . You can read about it at [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/omlink14/html/node1.html]

Here Are the Internet p Sites That I Promised You:

Believe it or not, this is just a sampling of what’s available on the Net. People are so obsessed with p .

· 200 Million Digits of Pi

ftp://www.cc.u-tokyo.ac.jp/pub/pi200m/pi200m.ascii

· 10 Million Digits of Pi

ftp://www.cc.u-tokyo.ac.jp/pub/pi10m/pi10m.ascii

· 100,000 Digits of Pi

http://www.geom.umn.edu/~huberty/math5337/groupe/digits.html

· Pi Search

http://www.aros.net/~angio/pi_stuff/piquery.html

· [The big one. The 51 billion]

http://www.lacim.uqam.ca/piDATA/Pi51billion.txt

· The Ridiculously Enhanced Pi PAGE
[This is the Exploratorium page — I recommend it]

http://www.exploratorium.edu/learning_studio/pi/pi.html

· A Slice of Pi Home Page http://www.geom.umn.edu/~huberty/math5337/groupe/welcome.html

· Am I in Pi?

http://www.facade.com/Fun/amiinpi/

· [hexadecimal expansion]

http://www.mathsoft.com/asolve/plouffe/announce.txt

· The Miraculous Bailey-Borwein-Plouffe Pi Algorithm

http://www.mathsoft.com/asolve/plouffe/plouffe.html

· [More hexadecimal details]

http://www.mathsoft.com/asolve/plouffe/elmntary.txt

· EARTH MYSTERIES: Notes on Pi

http://witcombe.bcpw.sbc.edu/EMPi.html

· PI

http://www.ccsf.caltech.edu/~roy/pi.html

· Search Pi

http://gryphon.ccs.brandeis.edu:80/~grath/attractions/gpi/index.html

· Jeremy Gilbert’s Homepage

http://gryphon.ccs.brandeis.edu/~grath/index.html

· Spinning Pi

http://gryphon.ccs.brandeis.edu/~grath/attractions/spin/

· [a prize is offered...]

http://www.ccsf.caltech.edu/~roy/episqrtn.html

· Danger! [I found this irresistible. And she knows her pi too!]

http://www.ugcs.caltech.edu/~eveander/eveanim.html

· The Garden of Eden

http://www.ugcs.caltech.edu/~eveander/

· The Pi Trivia Game

http://eveander.com/trivia/

· Links to Pi Pages

http://www.joyofpi.com/pilinks.htm

· The Joy of Pi

http://www.joyofpi.com/

· Inverse Symbolic Calculator

http://www.cecm.sfu.ca/projects/ISC/records.html

· The Pi Pages

http://www.cecm.sfu.ca/pi/

· Van Ceulen’s Home Page

http://sac.uky.edu/~ksmcke0/Van_Ceulen/

· Kelly McKenzie’s Home Page

http://sac.uky.edu/~ksmcke0/

· Archimedes’ Constant

http://www.mathsoft.com/asolve/constant/pi/pi.html

· Pi and Other Constants

http://www.cecm.sfu.ca/personal/pborwein/PISTUFF/Apistuff.html

· Resources

http://www.cecm.sfu.ca/projects/ISC/resources.html

· Directory of [4 billion, 200 million places of pi]

ftp://www.cc.u-tokyo.ac.jp/

· Favorite Mathematical Constants

http://www.mathsoft.com/asolve/constant/constant.html

· Table of Mathematical Constants

http://www.mathsoft.com/asolve/constant/table.html

· Table of Computation of Pi

http://www.cecm.sfu.ca/projects/ISC/Pihistory.html

· Yahoo! Science: Mathematics: Numerical Analysis: Numbers

http://www.yahoo.com/Science/Mathematics/Numerical_Analysis/Numbers/

· The Verbose Pi Page

http://avant.net/pi/

· Extraordinary Pi

http://www.users.globalnet.co.uk/~nickjh/Pi.htm

· Pi References

http://www.geom.umn.edu/~huberty/math5337/groupe/reference.html

· Infinite Expressions for Pi

http://www.geom.umn.edu/~huberty/math5337/groupe/expresspi.html

· PiHex Homepage

http://www.cecm.sfu.ca/projects/pihex/pihex.html

· Yet another story of pi

http://www.geocities.com/CapeCanaveral/Lab/3550/pi.htm

· The Pi Club

http://www.albanyconsort.com/pi/

· Fun Pi Facts

http://www.joyofpi.com/pifacts.htm

· Mathematics Archives — Numbers

http://archives.math.utk.edu/subjects/numbers.html

· William Schaaf on Pi

http://www.joyofpi.com/schaaf.htm

· Graf Theory

http://www-groups.dcs.st-and.ac.uk/~history/Miscellaneous/other_links/Graf_theory.html

· Nick Johnson-Hill’s Homepage

http://www.users.globalnet.co.uk/~nickjh/Pi.htm

· BIGGEST SELECTION OF PI LINKS ON THE INTERNET

http://www.users.globalnet.co.uk/~nickjh/pi_links.htm

· The Pi Page

http://www.ccsf.caltech.edu/~roy/pi.html

· Pi Through the Ages

http://www-groups.dcs.st-and.ac.uk:80/~history/HistTopics/Pi_through_the_ages.html

· The "Pi Is Rational" Page

http://www.slug.louisville.edu/~dsembr01/rationality-of-pi.html

· Al-Khowarithmi

http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Al'Khwarizmi.html

· Historical Overview of Pi

http://www.geom.umn.edu/~huberty/math5337/groupe/overview.html

· Archimedes’ Method

http://www.geom.umn.edu/~huberty/math5337/groupe/archimedean.html
Endnotes

1. Vincent Mallette, a student at the University of Chattanooga, presented this paper at the November, 1961 meeting of the Collegiate Division of the Tennessee Academy of Science and was awarded the highest place in the Physical Sciences Section

2. You can read all about it at [http://www.lacim.uqam.ca/piDATA/Pi51billion.txt] and at [http://www.cecm.sfu.ca/personal/jborwein/Kanada_50b.html]

The computer was a Hitachi SR2201; the run was done twice, with two different algorithms. One algorithm took about 25 hours and the other one about 37 hours. The work was done on various dates during June, July, and August of 1997. The last 10 digits of the first 50 billion are: 75109 30042 — if anyone cares. Incidentally, it would take 12,000 Bible-size books to contain the 50 billion digits, printed in 12-point type: [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/omlink3/html/node1.html]

3. W. W. Ball, Mathematical Recreations & Essays (revised by H. S. M. Coxeter) (New York: Macmillan, 1947), p. 339.

* Hereafter known as Ball, Recreations

4. David Eugene Smith, History of Mathematics (New York: Dover, 1958), Vol. II, p. 302.

* Hereafter known as Smith, History

5. Martin Gardner, Fads and Fallacies in the Name of Science (New York: Dover, 1957), p. 178. But Smith, History, is critical: Vol. I, p. 44

6. Smith, History, Vol. II, pp. 302-303

7. Smith, History, Vol. II, p. 307. Also Ball, Recreations, p. 341

8. Smith, History, Vol. II, p. 308. This was the Ptolemy (Claudius Ptolemaeus, c. 100 - c. 175 A.D.) who wrote the Almagest and saddled us with epicycles, etc.

9. Smith, History, Vol. I, p. 143

10. Smith, History, Vol. II, p. 309

11. Martin Gardner, "Incidental Information about the Extraordinary Number Pi," Scientific American, July 1960, p. 154

12. David Eugene Smith, "The History and Transcendence of p ," Monographs on Topics of Modern Mathematics ([New York]: Dover, 1955), p. 394. Also, Smith, History, Vol. II, p. 307

13. Smith, History, Vol. II, p. 309. Ball, Recreations, p. 342

14. Smith, History, Vol. II, pp. 308-309

15. I Kings, 7:23 — "And he made a molten sea, ten cubits from the one brim to the other: it was round all about..., and a line of thirty cubits did compass it round about." II Chronicles, 4:2 — "Also he made a molten sea of ten cubits from brim to brim, round in compass...; and a line of thirty cubits did compass it round about." King James version

16. Smith, History, Vol. II, p. 302 footnote

17. Martin Gardner, Fads and Fallacies in the Name of Science (New York: Dover, 1957), p. 178. I have read that the same ratio for the Pyramid of the Sun in Mexico is four times p , also very accurately. Thanks for this fact to Nick Johnson-Hill: [http://www.users.globalnet.co.uk/~nickjh/Pi.htm]. His home page is fascinating and informative.

18. I follow Smith, History, Vol. II, p. 307, but other sources very often give 240 B.C. for this date

19. Charles G. Fraser, Half-Hours with Great Scientists (New York: Reinhold, 1948), pp. 508-511. There are some nice graphics on Archimedes’ method at

http://www.geom.umn.edu/~huberty/math5337/groupe/archimedean.html

20. Smith, History, Vol. II, p. 309, paragraphs 3 and 5

21. Herman H. Harris, Jr., The History and Calculation of Pi (Volume 8, No. 1 in The Emporia State Research studies), p. 14

22. Ball, Recreations, pp. 343-344

23. Ball, Recreations, pp. 343-344

24. Ball, Recreations, pp. 343-344

25. Smith, History, Vol. II, p. 310. Howard Eves, An Introduction to the History of Mathematics (New York: Rinehart, 1953), p. 92. David Eugene Smith, "The History and Transcendence of p ," Monographs on Topics of Modern Mathematics ([New York]: Dover, 1955), p. 395

26. You can find out more than you want to know about Van Ceulen at [http://sac.uky.edu/~ksmcke0/Van_Ceulen/]

27. I have fudged a little here. Actually, Snell’s polygon contained 1,073,741,824 sides, and he obtained only 34 places from it. But Eves and Harris, in the works cited, both give Snell credit for duplicating Van Ceulen’s feat.

28. Ball, Recreations, p. 344

29. Howard Eves, An Introduction to the History of Mathematics (New York: Rinehart, 1953), p. 92.

* Hereafter known as Eves, Introduction

30. Alfred Hooper, Makers of Mathematics (New York: Random House [a Modern Library Paperback], 1948), p. 103. Herbert Westren Turnbull, "The Great Mathematicians," in The World of Mathematics — ed. by James R. Newman (New York: Simon and Schuster, 1956), p. 121

31. Ball, Recreations, p. 344

32. Ball, Recreations, p. 344

33. [http://www.geom.umn.edu/~huberty/math5337/groupe/overview.html]. There is a wealth of p information on the Internet; some of the better sites are listed at the end of this article.

34. H. von Baravalle, "The Number p ," The Mathematics Teacher, May 1952

35. David Eugene Smith, "The History and Transcendence of p ," Monographs on Topics of Modern Mathematics ([New York]: Dover, 1955), p. 397

36. David Eugene Smith, "The History and Transcendence of p ," Monographs on Topics of Modern Mathematics ([New York]: Dover, 1955), p. 396

37. Florian Cajori, A History of Mathematics (New York: Macmillan, 1929), p. 206

38. Ball, Recreations, pp. 364-365

39. Eves, Introduction, p. 94

40. Ball, Recreations, pp. 363-364

41. Ball, Recreations, p. 365; Eves, Introduction, p.94

42. Phillip S. Jones, "Miscellanea — Mathematical, Historical, Pedagogical," The Mathematics Teacher, March 1950, p.120

43. Phillip S. Jones, "Miscellanea — Mathematical, Historical, Pedagogical," The Mathematics Teacher, March 1950, pp. 120-121 and footnote 6 on p. 121

44. Quoted in Phillip S. Jones, "Miscellanea — Mathematical, Historical, Pedagogical," The Mathematics Teacher, March 1950, pp. 120-121

45. Quoted in Phillip S. Jones, "Miscellanea — Mathematical, Historical, Pedagogical," The Mathematics Teacher, March 1950, p. 120

46. Eves, Introduction, p. 94. You can see the title page of one of Shanks’ original books at [http://www.cecm.sfu.ca/cgi-bin/organics/getscan?target=/organics/papers/borwein/paper/html/local/scan_imgs/shanks1.gif]. Now there is a URL!

47. Ripley’s Believe It or Not, Garden City, 1946. My attention was directed to this by Mr. Joseph Saperstein.

48. Encyclopedia Britannica, 1952 edition, Vol. 14, p. 305

49. You can have a look at 10,000 nicely formatted p digits at [http://www.joyofpi.com/pi.htm]

And if you must indulge in wretched excess, you can gawk at 100,000 tightly packed digits at [http://www.geom.umn.edu/~huberty/math5337/groupe/digits.html]. If your thirst for p is still unslaked, you can pick up a million at [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/billdigits.html]. Then on your way home make arrangements to download 4 billion, 200 million digits from [ftp://www.cc.u-tokyo.ac.jp/]

50. Personal communication from Dr. Martin Ribarsky, our supercomputer expert here at Ga. Tech

51. If we say that Shanks spent a total of 15 years on his calculation, as Howard Eves does in An Introduction to the History of Mathematics (New York: Rinehart, 1953), p. 94

52. Also the father, or one of the fathers, of non-Euclidean geometry

53. There’s a nice little proof at [http://www.mcs.csuhayward.edu/~malek/Mathlinks/Pi.html]

54. Alexander Hellemans and Bryan Bunch, The Timetables of Science (New York: Simon and Schuster, 1988), p. 360

55. There are easier proofs of both the irrationality and transcendence by Niven: [http://www.aquest.com/~paris/pi.html#toc]. You can see a couple of pages of Lindemann’s original proof (in German!) at [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/lindemann.html]

56. Nine years before, Hermite had already proved the transcendence of e. But be warned. "The state of our ignorance is...profound. We do not know whether such basic constants as p + e, p /e or log p are irrational, let alone transcendental." "It is possible...that [most] of the decimal digits of p are in fact 0's and 1's" — Bailey, Borwein, and Borwein. Carl Sagan used some of this thinking in his novel Contact, for alien communication. [http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/node6.html#SECTION00020000000000000000]. Incidentally, Shanks died the year Lindemann proved the transcendence of p — was it some final despair that his beloved constant would never "come out even"?

57. "Since [1960] the digits of p have passed this test [for randomness] every time it has been run."— Paul Gusmorino [http://www.escape.com/~paulg53/math/pi/index.html]

Here is a concrete example of the distribution of digits from the first 6 billion places of p , courtesy of Nick Johnson-Hill: [http://www.users.globalnet.co.uk/~nickjh/Pi.htm]

0 occurs 599963005 times

1 occurs 600033260 times

2 occurs 599999169 times

3 occurs 600000243 times

4 occurs 599957439 times

5 occurs 600017176 times

6 occurs 600016588 times

7 occurs 600009044 times

8 occurs 599987038 times

9 occurs 600017038 times

(I performed the addition; the numbers add up to 6 billion.)

58. All this is adapted from Martin Gardner, "Incidental Information about the Extraordinary Number Pi," Scientific American, July 1960. The incomparable Martin Gardner has a recent book with a chapter on p : New Mathematical Diversions from Scientific American, Simon and Schuster

59. More of this sort of thing can be found in "The Universal Library," reprinted in Clifton Fadiman’s Fantasia Mathematica.

60. Tobias Dantzig, Number, the Language of Science (Garden City, New York: Doubleday Anchor, 1954), p. 119

61. Robert Edouard Moritz, compiler, On Mathematics and Mathematicians (former title: Memorabilia Mathematica) (New York: Dover, 1958), p. 373

62. School Science and Mathematics, Vol. 53, p. 106. The coda is from [http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html]

63. "Que j’aime à faire apprendre / Un nombre utile aux sages! / Immortel Archimède, artiste, ingénieur, / Qui de ton jugement peut priser la valeur! / Pour moi ton problème / Eut de pareils avantages." (Scientific American, Feb. 1956, p. 8). (Partial translation: "How I like to teach a number, useful to the learned: Immortal Archimedes, skillful investigator, yes, the number can tell the praise of your judgment....") H. von Baravalle, "The Number p ," The Mathematics Teacher, May 1952

64. Scientific American, Jan. 1956, p. 10; Feb. 1956, p. 8

65. This will give you the flavor of it, to some 63 places: "For a time I stood pondering on circle sizes. The large computer mainframe quietly processed all of its assembly code. Inside my entire hope lay for figuring out an elusive expansion. Value: pi. Decimals expected soon. I nervously entered a format procedure. The mainframe processed the request. Error. I, again entering it, carefully retyped. This iteration gave zero error printouts in all - success." Etc. Although stilted, it’s quite brilliant

66. James R. Newman, ed., The World of Mathematics (New York: Simon and Schuster, 1956), p. 2381, footnote

67. Eves, Introduction, p. 93

68. Ball, Recreations, p. 348

69. Augustus De Morgan, "Assorted Paradoxes," in The World of Mathematics — ed. by James R. Newman (New York: Simon and Schuster, 1956), p. 2382

70. Eves, Introduction, p. 94

71. Eves, Introduction, p. 94

72. Ball, Recreations, p. 349

73. This item is adapted from Phillip S. Jones, "Miscellanea — Mathematical, Historical, Pedagogical," The Mathematics Teacher, March 1950, p. 122. There is a very full treatment of this subject, including the complete text of the bill, at [http://daisy.uwaterloo.ca/%7Ealopez-o/math-faq/mathtext/node18.html] and also at [http://www.urbanlegends.com/legal/pi_indiana.html]; this latter source has annotations. In addition, Ilan Vardi’s site was quite valuable [http://www.oxy.edu:80/~ilan/pi.html]. It seems that different interpretations of the murky and self-contradictory wording of the proposed law can yield as many as four different values for p , all grossly incorrect of course, viz 3; 3.2; 4; and 9.2376.... The Guinness Book of Records (see footnote below) cites the de jure value as 4, which agrees with my reading of the relevant passages. But of course it doesn’t really matter. Had Indiana been saddled with this barbarous law, the legislators would have been forced to drive on square wheels the rest of their days.

74. Eves, Introduction, p. 106

75. The Guinness Book of Records 1993 — ed. by Peter Matthews (New York: Bantam Books, 1993), p. 193

76. See article "The Indiana Pi Law" on the Inwit web pages

77. Thank you, Steve Berlin [http://www.ugcs.caltech.edu/~eveander/wst.html]

78. Carl B. Boyer, The History of the Calculus and Its Conceptual Development (New York: Dover, 1959), p. 262

79. The World Almanac and Book of Facts 1997 — edited by Robert Famighetti et al [Mahwah, New Jersey: World Almanac Books (an imprint of K-III Reference Corporation), 1996]. ISBN 0-88687-800-4 (softcover)

80. W. W. Rouse Ball, A Short Account of the History of Mathematics (London: Macmillan, 1935), p.395

81. Herbert Westren Turnbull, "The Great Mathematicians," in The World of Mathematics — ed. by James R. Newman (New York: Simon and Schuster, 1956), p. 151

82. I wonder if he used some of the protocols of the infamous Indiana bill (see above), since 3.2 is one of the false values that can be extracted from the bill’s wording

83. New York: Rinehart, 1953, p. 95

84. [http://eveander.com/trivia/index.cgi?25]

85. A professional treatment is available at [http://www.cecm.sfu.ca/organics/papers/borwein/index.html]

86. [http://www.mcs.surrey.ac.uk/Personal/R.Knott]

87. The Miraculous Bailey-Borwein-Plouffe Pi Algorithm:

[http://www.mathsoft.com/asolve/plouffe/plouffe.html]

88. Nick Johnson-Hill, [http://www.users.globalnet.co.uk/~nickjh/Pi.htm]

89. Merriam-Webster New International Dictionary, 2nd ed., article "Pi."

90. Florian Cajori, A History of Mathematics (New York: Macmillan, 1929), p. 158

91. W. W. Rouse Ball, A Short Account of the History of Mathematics (London: Macmillan, 1935), p. 394

92. periphery in Greek beginning with p and diameter with d

93. Smith, History, Vol. II, p. 312

94. Smith, History, Vol. II, p. 312

95. Smith, History, Vol. II, p. 312. Also, David Eugene Smith, ed., A Source Book in Mathematics (1st edition) (New York: McGraw-Hill, 1929), pp. 346-347

96. This also seems to anticipate radian measure, where p radians = 180° (180° being of course half a circle’s periphery). The interesting thing is that radians were not formally invented until more than 150 years later. But it would be a natural concept for Jones to employ, since radians, implicitly or explicitly, lie at the heart of virtually every formula for computing p

97. Ball, Recreations, p. 338

98. Ball, Recreations, p. 338

99. Ball, Recreations, p. 338

100. Smith, History, Vol. II, p. 312

101. W. W. Rouse Ball, A Short Account of the History of Mathematics (London: Macmillan, 1935), p. 395

102. Ball, Recreations, p. 338; Smith, History, Vol. I, p. 522

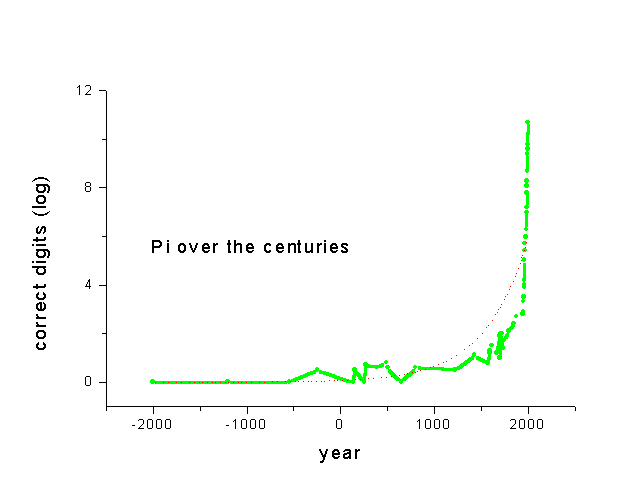
Figure 1. The number of correct digits of p achieved, as a function of time (the logarithm of the digits was plotted). The thin dotted line is the best fitting curve of true exponential growth. Note that between the year 1000 and, say, 1980, the achievement curve actually grows more slowly than the exponential. Those digits — hand calculated until 1947 — were hard won. The nearly vertical take-off after 1947 reflects the invention of the electronic computer. The triangular jog around 250 B.C. is of course Archimedes; the uplift in the first half-millennium is due to Ptolemy and various Oriental savants, including the motorboat man, Tsu-Ch’ung-chih. (Data and inspiration from David H. Bailey, Jonathan M. Borwein, Peter B. Borwein and Simon Plouffe [http://www.cecm.sfu.ca/pi/piquest/].

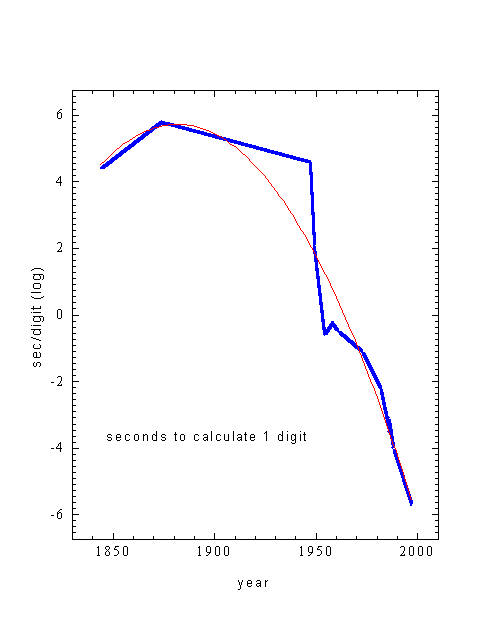
Figure 2. An idea that would never have occurred to me: the time required to calculate 1 digit of p . I owe the idea (and the data!) to Neal Carothers [http://ernie.bgsu.edu/~carother/pi/Pi2a.html]; the data are also available at Dale Winham’s [http://www.geocities.com/SiliconValley/Pines/5945/charts.html].

Here you see a plot of the number of seconds, or fractions of a second, required on average to calculate 1 digit. The time varies from 1 week per digit for poor hapless Shanks (about ²/₃ of a "megasecond" per digit) to less than 2 microseconds per digit for the latest Japanese supercomputer. The first data point is Dase; he took about 7 hrs/digit. Shanks took 7 days/digit. Shanks’ algorithm was no worse than Dase’s, but Dase had the advantage of being the greatest mental calculator who ever lived.

The extremely steep drop around 1947 — faster even than an exponential — is once again the contribution of the electronic computer. After that there is a slowdown as computers begin to come up against their own limits; the smooth curve fits quite closely from about 1970 to the present.

INWIT™

INWIT™ WRITINGS, LINKS AND SOFTWARE DEMONSTRATIONS

WATKINS COMPANIES

Copyright © 1982-2024 Christopher D. Watkins. All Rights Reserved. LEGAL
Orlando, Florida, USA | Thu 19 Apr 2018